-
Propriétés des opérations :
Commutativité : x*y = y*x
Associativité : (x*y)*z = x*(y*)
Elément neutre : x*e = e*x = x
Symétrique : loi * dispose d’un élément neutre e => x possède un symétrique s’il existe xs tel que
x*xs = xs*x = e
Distributivité : x*(y°z) = (x*y) ° (x*z)
Addition dans N :
Définitions :
-soit 2 ensembles disjoint A de cardinal a et B de cardinal b => a+b = Card(AÈB)
-a+b = s, où s = b sauts sur droite numérique à partir de a vers la droite
Propriétés : commutative, associative, élément neutre = 0, compatible avec relation d’ordre. On peut ajouter membre à membre 2 inégalités de même sens
Multiplication dans N :
Définitions :
-produit cartésien ensemble A x ensemble B, Card(A) x Card(B)
-axb = somme b+b+b+b… où b apparaît a fois
Propriétés : commutative, associative, élément neutre = 1, distributive sur addition et soustraction, compatible avec relation d’ordre. On peut multiplier membre à membre 2 inégalités de même sens (nb entiers positifs)
Soustraction :
Définitions :
- soit un ensemble A de cardinal a, composé d’un ensemble B de cardinal b et d’un ensemble C de cardinal c => a-b = Card(A)-Card(B) = Card(C)
- a-b = d où d = b sauts sur droite numérique à partir de a vers la gauche
La soustraction n’est pas une loi de composition interne car ne fonctionne que pour a > ou = b
Propriétés : compatible avec relation d’ordre, propriété des différences égales : pas de modification d’une soustraction en ajoutant un même nb à ses 2 termes (n’est pas commutative, ni associative, pas d’élément neutre)
Division euclidienne :
Définition : diviser a/b = chercher q tel que a = b x q + r (a = dividende, b = diviseur, q = quotient, r = reste)
Si a/b = q => division à quotient exact
Division euclidienne n’est pas une loi de composition interne car à tout couple d’entiers (a ; b) elle associe un autre couple (q ; r)
Opérations dans Z, D, Q et R :
Addition : reste une loi de composition interne. Reste commutative, associative et élément neutre = 0, compatible avec relation d’ordre. Mais chaque élément dispose aussi d’un symétrique (opposé).
Multiplication : reste une loi de composition interne. Reste commutative, associative et élément neutre = 1. N’est pas compatible avec relation d’ordre que sur Z+, D+, Q+ et R+. Dans Z, seul 1 possèdent un symétrique : lui-même. Dans Q et R, tous éléments non nuls ont un symétrique (inverse) : a-1 ou 1/a. Dans D, certains éléments possèdent un inverse.
Soustraction : est cette fois une loi de composition interne. Compatible avec relation d’ordre, mais on ne peut pas soustraire membre à membre 2 inégalités de même sens, propriété des différences égales (pas commutative ni associative)
Division dans Q+ et R+ : diviser a/b = rechercher nb q tel que b x q = a => nb q = a x b-1. Pas commutative ni associative, pas d’élément neutre. Compatible avec relation d’ordre dans Q+ et R+.
Résolution d’équations et d’inéquations :
Equation du 1er degré : a X x + b = c X x + d
Résolution : regrouper d’un côté du = les termes où figure l’inconnue, de l’autre ceux où elle n’apparaît pas.
Système de 2 équations à 2 inconnues : résolution :
-éliminer une inconnue dans une des équations => équation du 1er degré où x = seule inconnue : par substitution (isoler x d’un côté du =, y de l’autre => exprimer y en fonction de x => remplacer y par cette expression), par combinaison linéaire (multiplier la première équation par nb qui multiplie x dans la seconde, et la seconde par nb qui multiplie x dans la première => même coefficient multiplicateur devant x dans les 2 équations => soustraire membre à membre les 2 équations => x et son facteur sont identiques des 2 côtés du = et donc s’annulent)
-reporter valeur de x dans seconde équation pour trouver y
Inéquation du 1er degré : résolution :
-idem début résolution équation 1er degré (passer inconnue d’un côté du =)
-isoler l’inconnue
Preuves d’une opération :
Contrôle de l’ordre de grandeur :
-avec classe d’unité à laquelle appartient chiffres dans système numération base 10
-avec dizaine/centaine/millier… plus proche
Calcul inverse :
Division => multiplication (vérifier que D = d X q + r et r < d pour prouver D/d)
Soustraction => addition (vérifier b + c = a pour prouver que a – b = c)
Preuve par 9 :
Reste dans la division /9 d’un nb entier = reste de la division /9 de la somme de ses chiffres. Si elle échoue : résultat = faux, si elle réussit résultat n’est pas forcément juste.
Pour multiplication :
-calcul somme des chiffres différents de 9 (reste) pour le multiplicande (en haut), résultat (gauche), et multiplicateur (en bas), puis du produit de restes du haut et du bas (droite)
-chiffre de droite et de gauche doivent être égaux
Pour division :
-calcul reste du diviseur (en haut), du dividende (gauche), du quotient (bas) puis du produit des restes chiffres du haut et du bas (droite)
-chiffres de droite et de gauche doivent être égaux
Contrôle du chiffre des unités :
-a+b=c : chiffre des unités de c = somme chiffres des unités de a et b
-aXb=c : chiffres des unités de c = chiffre des unités du résultat du produit des chiffres des unités de a et b
Contrôle des 2 derniers chiffres : idem qu’avec chiffres des unités
Calcul littéral :
Développer = transformer expression algébrique en une somme de produits la plus courte possible : utilisation de la distributivité et règles des signes pour les produits.
Factoriser = écrire une expression algébrique sous la forme d’un produit de facteurs.
Identités remarquables :
(a + b)² = a² + 2ab + b²
(a – b)² = a² - 2ab + b²
(a + b)(a – b) = a² - b²
Equations du second degré : ax² + bx + c = 0
X0 est solution si (x – x0) peut y être mis en facteur
L’équation a 2 solution, x1 et x2 => l’expression peut se factoriser sous la forme a(x – x1)(x – x2)
L’équation n’a qu’une solution x0 => l’expression peut se factoriser sous la forme a(x – x0), et x0 = racine double de l’équation
L’équation n’a pas de solution => l’expression ne peut pas se factoriser
L’équation x² = a admet 2 solutions : √a et -√a
Liens cours: http://www.parimaths.com/telechargements/methodes/pdf/M3-Calcul-Numerique-et-Litteral.pdf
http://plates-formes.iufm.fr/alsace/moodle/mod/resource/view.php?id=1231(calcul et opérations)
Liens exercices: http://www.parimaths.com/telechargements/cours-exercices/pdf/S3-Calcul-Numerique.pdf
http://www.parimaths.com/telechargements/corriges/pdf/S3C-Calcul-Numerique.pdf (corrigé)
http://www.parimaths.com/telechargements/cours-exercices/pdf/S4-Calcul-litteral.pdf
http://www.parimaths.com/telechargements/corriges/pdf/S4C-Calcul-litteral.pdf (corrigé)
http://www.parimaths.com/telechargements/cours-exercices/pdf/S5-Calcul-algebrique.pdf
http://www.parimaths.com/telechargements/corriges/pdf/S5C-Calcul-algebrique.pdf (corrigé)
http://plates-formes.iufm.fr/alsace/moodle/mod/resource/view.php?id=1249 (calcul et opérations)
votre commentaire
-
1- L’ensemble N des nombres naturels
N : { 0, 1, 2, 3, 4…n, n+1}
1-1. Caractérisation
Une définition du nombre comme cardinal qui implique de préciser la notion d’ensembles équipotents. 2 ensembles sont équipotents si on peut établir une bijection (correspondance terme à terme) entre eux. Le nombre cardinal est le représentant de tous les ensembles qui sont équipotents entre eux ; ainsi le nombre « 2 » est le représentant de toutes les collections qui sont constituées par une paire d’éléments. Dans le cadre de collections finies le cardinal est synonyme du nombre d’éléments…
Une définition du nombre comme un élément d’une suite organisée qui possède les propriétés suivantes (aspect ordinal) :
- chaque élément a un successeur unique appartenant à cet ensemble ( le successeur de n peut être noté n+1) ;
- deux éléments différents ont des successeurs différents ;
- 0, appartenant à cet ensemble, n’est le successeur d’aucun nombre ;
- toute partie de N vérifiant ces propriétés et contenant 0 est égale à N.
1-2. Propriétés dans N
L’ensemble N peut être muni de lois de composition interne qui permettent à tout couple de naturels d’associer un autre naturel ; c’est le cas notamment de l’addition et de la multiplication.
· L’addition fait correspondre à tout couple (a, b) de N x N le nombre noté a + b appartenant à N :
- du point de vue cardinal, la somme a + b est associé à la réunion de 2 ensembles disjoints qui ont respectivement a et b éléments.
- Du point de vue ordinal, la somme a + b représente le nombre qui se situe b après a
L’addition dans N est :
- associative (a + b) + c = a + (b + c)
- commutative : a + b = b + a
- régulière : si a + c = b + c, alors a = b
- elle possède 0 comme éléments neutre : a + 0 = 0 + a = a.
· la multiplication fait correspondre à tout couple (a, b) de N x N le nombre noté a x b appartenant à N :
- du point de vue cardinal, le produit a x b est associé au cardinal du point cartésien de 2 ensembles
- du point de vue ordinal, le produit a x b est associé au b-ième terme de la suite de a en a à partir de 0.
La multiplication dans N est :
- associative : ( a x b ) x c = a x ( b x c )
- commutative : a x b = b x a
- régulière : si c ≠ 0 : a x c = b x c => a = b
- distributive par rapport à l’addition : a x ( b + c ) = ( a x b ) + ( a x c )
- le nombre 1 est élément neutre : a x 1 = 1 x a = a
- 0 est élément absorbant : a x 0 = 0 x a = 0.
· L’ensemble N est ordonné par une relation qui permet de comparer les nombres :
a < b si et seulement s’il existe c appartenant à N, tel que b = a + c
Cet ordre correspond :
- du point de vue cardinal, au fait que l’ensemble A (de cardinal a) a moins d’éléments que l’ensemble B (de cardinal b) ;
- du point du vue ordinal au fait que « a est situé avant b dans la suite de nombres. »
Cet ordre est compatible avec l’addition et la multiplication par un naturel non nul :
Si a > b, alors a + c > b + c et si c ≠ 0, alors a x c > b x c. L’ordre est total : tous les nombres entiers naturels peuvent être comparés 2 à 2 avec cette relation.
Ces propriétés sont aussi vérifiées dans les autres ensembles Z, Q, D, R.
- N est un ensemble infini
Un ensemble infini est dit dénombrable s’il peut être mis en bijection avec N L’ensemble des nombres pairs est dénombrable : il est infini et a «autant » d’éléments que N.
1-2. Les insuffisances de N
la soustraction n’est pas toujours possible : x = a – b (défini par b + x = a) n’a de solution dans N que si a > b ; certaines équations du type b + x = a n’ont donc pas de solution dans N.
2- l’ensemble Z des nombres entiers.
Cet ensemble permet de pallier en partie ces insuffisances : les entiers peuvent permettre de graduer la droite et l’équation b + x = a a toujours une solution dans cet ensemble.
2-1. Caractérisation
L’ensemble des nombres entiers relatifs complète l’ensemble des nombres naturels.
Z : {…,-n,…, -2, -1, 0, 1, 2, …, n, …}
Les nombres relatifs sont étudiés dans différents contextes : températures, altitudes ou profondeurs, dates, ascenseurs, gains ou pertes, repérage d’une droite…
0 est à la fois positif et négatif.
L’ensemble des nombres différents de 0 est noté Z* ;
L’ensemble des nombres relatifs positifs est noté Z+ ;
L’ensemble des nombres relatifs négatifs est noté Z.
Si x appartient à Z un seul des 2 éléments de { x, -x } est dans N, il est appelé valeur absolue de x et noté │x│ ; │x│ = x si x > 0 et │x│ = - x si x < 0.
2-2. Propriétés dans Z
- l’addition dans Z (qui est associative et commutative) possède un élément neutre 0 et tout élément x a un opposé x’, qui vérifie x + x’ = x’ + x = 0 et est noté – x.
Ex : l’opposé de 3 et –3 ; l’opposé de –2 est (-2), cad 2 ; l’opposé de x est –(- x), cad x.
La multiplication des entiers relatifs vérifie les propriétés déjà établies dans N.
- La multiplication des entiers relatifs vérifie les propriétés déjà établies dans N.
La règle des signes :
Le produit de 2 relatifs s’obtient à partir du produit de leur valeur absolue et en utilisant la règle des signes :
- le produit de 2 nombres positifs est positif ;
- le produit de 2 nombres négatifs est positif ;
- le produit d’un nombre positif par un nombre négatif est négatif.
- L’ordre de Z prolonge celui de N : il est compatible avec l’addition, la multiplication par un entier est strictement positif.
Si c > 0 et a < b, alors a x c < b x c
Si c < 0 et a < b, alors a x c > b x c
D’autre part si a < b et c < d , alors a + c < b + d
Ex : -7 < -3 donc 2 x (-7) < 2 x (-3), donc –14 < -6
Contrairement à N, Z n’a pas de plus petit élément.
- Comparaison des nombres relatifs : l’ensemble des relatifs est muni d’un ordre total.
- si 2 nombres relatifs sont de signe opposé, le nombre positif est plus grand ( 5 > -8)
- si les 2 nombres sont négatifs, le plus grand est celui qui a la plus petite valeur absolue ( -2 > -5) ;
- si les 2 nombres sont positifs, le plus grand est celui qui a la plus grande valeur absolue.
- Les nombres relatifs peuvent être représenté sur une droite numérique :
- L’ensemble des nombres relatifs est dénombrable
On peut établir une bijection entre Z et N : il y a donc « autant » d’éléments dans Z que dans N :
2-2. les insuffisances dans Z
- certaines équations a x x = b n’ont pas de solution dans Z, comme par exemple 2 x x = 5.
- Les nombres entiers relatifs, sauf 1 et –1 n’ont pas d’inverse pour la multiplication.
3- L’ensemble Q des nombres rationnels
Cet ensemble permet de pallier en partie les insuffisances constatées deans les ensembles précédents.
3-1. Caractérisation
Un rationnel est un nombre x qui est solution d’une équation b x x = a, avec a et b entiers et b ≠ 0.
Ce nombre x peut s’écrire sous la forme a/b, le nombre a étant le numérateur de la fraction, le nombre b le dénominateur et a/b le quotient de a par b.
- Fractions égales : 2 fractions a/b et c/d sont égales si elles représentent le même rationnel ; on a alors a x d = b x c ( on dit qu’on a fait le produit en croix).
- Simplification de fraction : une fraction peut être simplifiée en divisant son numérateur et son dénominateur par un diviseur commun. Une fraction est irréductible si le numérateur et le dénominateurs sont premiers entre eux. En divisant le numérateur et le dénominateur par le PGCD, la fraction obtenue est irréductible.
Un nombre rationnel peut être représenté par une infinité de fractions égales. Si a/b est une fraction irréductible, les autres fractions égales sont de la forme (k x a) / (k x b) avec k entier relatif différent de 0.
Par ex : 14/4 = 35/10 = 77/22. La fraction « irréductible » ou « réduite » égale à 14/4 est 7/2. Les fractions égales seront sous la forme (7 x k) / (2 x k) avec k appartenant à Z*.
La décomposition en facteurs premiers du numérateur et du dénominateur peut faciliter la simplification des fractions.
Par ex : 440 = 23 x 5 x 11 = 5 x 11 = 55
336 24 x 3 x 7 2 x 3 x 7 42
3-2. Propriétés dans Q
- Tout élément non nul a un inverse pour la multiplication.
L’inverse de a est b , car a x b = 1 donc 1 = b
b a b a a a
b
- La somme et le produit de 2 rationnels a et b sont des rationnels, ainsi que leur différences avec le quotient. On dit que l’ensemble des rationnels est clos pour l’addition et la multiplication et leurs opérations réciproques ; Q est le plus petit entier qui vérifie cette propriété.
- Pour additionner ou soustraire des fractions :
- si les dénominateurs sont égaux, on additionne les numérateurs :
a/b + c/b = (a+c)/b
- si les dénominateurs sont différents, on cherche d’abord un dénominateur commun; pour cela on recherche un multiple commun aux dénominateurs, le PPCM
ex : 1/14 – 9/16
le PPCM de 14 et 16 et 112 (14=2x 7 et 16 = 2^4 ; le ppcm de 14 et 16 est 2^4 x 7 = 112) ; 1/14 + 9/16 = 8/112 – 63/112 = (8-63)/112 = -55/112
- Pour multiplier une fraction par un entier, on multiplie le numérateur par cet entier.
- Pour multiplier 2 fractions entre elles, on multiplie les numérateurs entre eux et les dénominateurs entre eux ; on peut être amené à simplifier la fraction, au cours du calcul ou à son terme.
- Pour diviser une fraction par une autre, on multiplie la première par l’inverse de la deuxième.
a x c = a x c a x c = a x c a / c = a x d
b b b d b x d b d b c
- L’ensemble des nombres rationnels est totalement ordonné : si a et b sont 2 rationnels, on a : a > b ou b > a.
- si les dénominateurs sont égaux, on compare les numérateurs : la fraction la plus grande est celle qui a le plus grand numérateur.
- Si les numérateurs sont égaux, on compare les dénominateurs : la fraction la plus grande est celle qui a le plus petit dénominateur.
- Dans certains cas il est préférable de procéder par majoration ou minoration de certaines expressions
- On peut procéder par un encadrement des entiers, par des fractions
- En général , la méthode de comparaison de 2 rationnels exprimés par des fractions consiste à réduire les fractions au même dénominateur.
- L’intervalle ]a, b[ (ensemble des rationnels q tels que a < q < b) possède une infinité d’éléments.
- Il y a autant d’éléments dans Q que dans N
- Tout rationnel est approchable par un décimal avec une précision aussi grande que l’on veut.
- Les rationnels permettent de compléter la graduation d’une droite.
3-2. Insuffisances de Q
- La mesure d’une longueur, en utilisant une autre longueur qui sert d’unité ne s’exprime pas toujours avec un nombre rationnel.
- Certains rapports, comme celui entre les mesures et de la circonférence d’un cercle, ne peuvent s’exprimer à partir de nombres rationnels.
4- L’ensemble D des nombres décimaux
La comparaison ou le calcul avec les rationnels écrits sous forme fractionnaire sont souvent longs. Mais ils sont plus simples pour certains types de fractions, notamment celles dont les dénominateurs sont écrits avec les puissances de 10
4-1. Caractérisation
un nombre a est décimal s’il existe un entier naturel n
tel que a x 10n soit un entier relatif à b.
a x 10n = b ; donc a = b / 10n
4-2 Propriétés
- L’ensemble des décimaux est stable par l’addition et la multiplication
L’ensemble ou le produit de 2 nbres décimaux sont des nombres décimaux. L’opposé -x d’un nombre décimal x est un nbre décimal. Mais l’inverse 1/x d’un nb décimal x non nul n’est pas toujours un nb décimal : 0,3 (ou 1/10) est un nb décimal, mais son inverse 10/3=3.3333…(avec une infinité de 3 ne l’est pas.
- Comparaison des décimaux : pour comparer 2 nb décimaux, on comparer les parties entières, puis respectivement chaque chiffre des parties décimales, à partir des dixièmes.
- Densité : entre 2 décimaux on peut toujours trouver un nb décimal.
5- L’ensemble R des nombres réels
5-1. Caractérisation
l’ensemble R des nb réels est un ensemble « continu », cad qu’on peut établir une bijection entre les pts des la droite et les nb réels. Les nb réels permettent de graduer parfaitement, sans trou, la droite.
Ex pi, racine de 2…
5-2. Propriétés
Les propriétés vérifiées dans Q e sont aussi dans R ; en particulier tout élément non nul a un inverse pour la multiplication.
Tout réel peut être approché d’aussi près que l’on veut à l’aide des nb décimaux.
5-3. Puissances dans R
Qques rappels concernant les puissances entières
5-4. Calculs sur les radicaux
Conclusion :
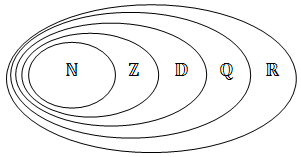
N est inclus dans Z ; Z est inclus dans D ; D est inclus dans Q ; Q est inclus dans R ;
6- Ecritures décimales
6-1. Fraction décimale
Les seuls rationnels qui sont des décimaux sont donc ceux qui peuvent s’écrire à l’aide d’une fraction irréductible dont le dénominateur est composé par le produit d’une puissance de 2 par une puissance de 5.
6-2. Ecritures décimales
Une écriture décimale peut désigner : un entier (3.00), un décimal (3.2), un rationnel non décimal (0.3333…) avec une infinité de 3 est égal à 1/3), ou irrationnel (racine carrée de 2= 10414…). Il ne faut donc pas confondre « nb décimal » et « écriture décimale ».
- L’écriture décimale de x est finie : elle comporte un nb fini n de chiffres non nul après la virgule : x x 10^n est un entier, le nb x est décimal par déf.
- x est un rationnel non décimal
- Réciproquement si une suite est périodique et illimitée, elle est l’écriture d’un nb rationnel.
- Cas particulier
- Une écriture décimale illimitée mais non périodique sera l’écriture d’un nb irrationnel et non pas d’un rationnel.
Ex : 0.100011000111000011110000011111…
En conclusion
A tout rationnel correspond une écriture décimale ou une suie décimale illimitée périodique et à toute suite décimale illimitée périodique correspond un nb rationnel.
Liens utiles: http://www.e-crpe.com/ ici de nombreux cours vidéos dans les onglets "numération" et "algèbre".
1 commentaire
-
LES FORMES DU VERBE
I. Le système des formes verbiales
- 3 groupes
- 3 voix (formes): actif (il lave), passif (il est lavé), pronominale (il se lave)
- 3 personnes au singulier + 3 personnes au pluriel
- 4 modes personnels: indicatif, subjonctif, impératif, conditionnel
- 3 séries de temps: 5 temps simples (présent, imparfait, futur simple, passé simple, conditionnel présent), 5 temps composés (passé composé, plus-que-parfait, futur antérieur, passé antérieur, conditionnel passé), 2 temps sur-composés (passé surcomposé, futur antérieur surcomposé >> à ne pas prendre en compte pour l'école primaire)
* Conjugaison d'un verbe: 191 formes
> 90 formes personnelles actives: 60 formes d'indicatif ( 6 pers X 10 temps d'indicatif) + 24 formes du subjonctif (6 pers X 4 temps du subjonctif) + 6 formes d'impératif ( 3 pers X 2 temps)
> 6 formes des modes impersonnels correspondant aux: 2 formes d'indicatif (simple, chanter et passé, avoir chanté) + 3 formes de participe (présent, chantant, passé forme simple, chanté et forme composé, ayant chanté) + 1 forme de gérondif (en chantant)
> 95 formes passives pour les verbes qui ont un passif.
II. Les différents éléments d'une forme verbale
A. Radical au base: élément fondamental du verbe
Elément commun à toutes les formes verbales qui appartiennent à la conjugaison d'un verbe.
Base: désigne les formes différentes que peut prendre un radical: finir > 2 bases: fini & finiss
B. La désinence au terminaison: apporte les infos grammaticales
Il existe 3 morphèmes grammaticaux:
- 12 morphèmes de la personne et du nombre: -e, -es, -s, -x, -t, -ent, -ons, -ez, -as, -a, -ai >> seulement 5 morphèmes différents à l'oral.
- morphème -(e)r- : caractérise les formes du futur et du conditionnel
- morphème -ai ou -i : caractérisent l'imparfait, le conditionnel
Les morphèmes se combinent après le radical: il jouerait, 3° pers du sing du conditionnel présent
1base jou et 3 morphèmes: -er (il s'agit d'un futur ou d'un conditionnel), -ai (indique le conditionnel par rapport au futur), -t (indique la personne verbale)
LES EMPLOIS DU VERBE
I. L'emploi des temps verbaux est lié à la situation d'énonciation
A. Système d'énonciation de Benveniste
Il explique l'emploi du temps verbaux en relation avec la situation d'énonciation:
> énonciation du discours: le locuteur s'implique dans son énoncé.
> énonciation de récit (ou historique): le locuteur se détache de son énoncé.
Le récit
Enonciation historique
Le discours
Enonciation du discours
- Aucune intervention du locuteur dans le récit (événements semblent se raconter eux-mêmes)
- Evénements présentés comme passés, antérieurs à la narration
- Seules les personnes 3 (il, elle, on) et 6 (ils, elles) sont concernées
- Temps fondamental: passé simple, imparfait, plus-que-parfait, conditionnel présent > vérité générale + historique
- Exclut tout indicateur de temps et de lieu qui renvoit au moment de l'énonciation (aujourd'hui, ici
- Quelqu'un s'adresse à quelqu'un
- Relation de faits, commentaires, témoignage
- Emploi de toutes les formes personnelles des verbes (toutes les personnes)
- Tous les temps sont possibles sauf le passé simple remplacé par le passé composé
- Accepte les références à la situation d'énonciation
II. La valeur du temps
A. Les valeur du présent
Présent énonciatif lié au locuteur qui s'exprime et contemporain du moment de l'énonciation - Coïncidence entre l'évènement et le moment de parole - <!!!> Le présent peut déborder sur le futur (Je m'en vais dans cinq minutes) et sur le passé (J'apprends le solfège depuis deux ans)
Présent de vérité générale (discours): il prend une valeur atemporelle ou omnitemporelle qui englobe toutes les époques (L'eau bout à 100 degrès. L'homme est un loup pour l'homme) - Présent des dictons, proverbes (Qui vole un oeuf vole un boeuf).
Présent de narration (dans l'énonciation historique > récit) évoque les évènements passés qui sont détachés du moment de l'énonciation (Un agneau se désaltérait, un loup survient à jeun qui cherchait aventure)
B. Le couple imparfait/passé simple dans l'énonciation historique > récit
Sert à situer des procés (actions exprimées par le verbe) dans le passé. Leur différence est aspectuelle: aspect bormé (procés pris entre des limites temporelles) et non-borné (aucune limite), aspect accompli et inaccompli.
Imparfait: situe le procés dans le passé, le montre comme perçu de l'intérieur, en cours d'accomplissement. Sans bornes ni limites bien marquées. Sert à poser les faits d'arrière-plan, la toile de fond, le décor: Il faisait beau ce jour-là. La ville était calme.
Passé simple: installe aussi le procés dans le passé, mais le présente comme un tout bien circonscrit. En donne une vision bormée qui prend en compte le début et la fin de l'action. Durée plus ou moins longue: Il fuma une cigarette. Rome domina le monde pendant des siècles.Ces deux temps s'accordent bien pour exprimer la simultanéité de deux phénomènes.
C. Le passé composé dans l'énonciation du discours et dans la narration liée
3 valeurs du passé composé:
- Expression d'une action accomplie dans le présent: Il est arrivé
- Expression d'une action antérieure au présent: Quand il a déjeuné, il fait la sieste.
- Expression du passé: Le temps était beau et nous avons fait une promenade.
D. L'expression de la visée prospective
Futur
2 formes: futur simple et futur proche avec le verbe aller ou devoir conjugué au présent (Je dois partir > valeur temporelle, indique une projection de l'anonciateur dans l'avenir)
Il possède d'autres valeurs et peut exprimer:
- engagement, promesse: Je te dirai toute la vérité, rien que la vérité.
- consigne: A partir de ces 3 textes, vous rendrez compte de la complexité...
- ordre: Tu ne tueras point.
- prédiction: Il ne dira rien.
- énonciation proverbiale: Qui vivra verra. > valeur omnitemporelle
Futur narratif = même valeur que le présent de narration: se détache de la situation d'énonciation.
Conditionnel
Enonciation de discours
Le conditionnel peut être en concurrence avec le futur.
Elle pense que son ami viendra / Elle pense que son ami viendrait.
> Le conditionnel marque une probabilité moindre que celle exprimée par le futur.
Narration liée à l'énonciation historique
Couplé avec les temps du passé (imparfait, passé composé), le conditionnel sert de futur dans le passé.
Je savais qque c'était stupide, que je ne me débarasserais pas du soleil en me déployant...
Expression de la visée rétrospective (fait se retrouner vers le passé)
Enonciation de discours
Passé récent: le verbe venir au présent + préposition de + infinitif Il vient de partir
Narration liée à l'énonciation historique
verbe venir à l'imparfait + préposition de + infinitif Il venait de partir
Expression de l'antériorité
Le passé composé sert à exprimer l'aspect accompli + antériorité. Les autres temps composés de l'indicatif possèdent aussi ces valeurs par rapport à leurs temps simples correspondants
Imparfait Plus que parfait Il s'amusait quand il avait fini son travail.
Passé simple Passé antérieur Il s'amusa quand il eut fini son travail.
Futur simple Futur antérieur Il s'amusera quand il aura fini son travail.
III. Fonction modale
Le verbe possède une fonstion modale qui révèle l'attitude du sujet partout à l'égard de son énoncé.
A. L'expression de la modalité ne se confond pas avec les modes
Indicatif: peut exprimer des procés comme simplement envisagés, virtuels (Il me promet qu'il apprendra ses leçons)
Alors que le subjonctif peut situer des faits réels (Les camions circulent bien que les barrières de dégel soient en place)
Présent, futur: éventualité > futur J'espère qu'il viendra.
> futur antérieur Paul est en retard, il aura encore oublié le rendez-vous.
Conditionnel: parfois considéré comme un temps et non plus comme un mode.
Impératif: Il y a des nuances; dans La Marseillaise, Marchons, il s"agit plus d'un ordre.
Subjonctif: inapte à la fonction temporelle, beaucoup plus douée pour exprimer des valeurs. Il est employé quand:
- l'interprétation l'emporte sur la prise en compte de l'actualisation du procés.
- il s'interpose entre le procés et sa verbalisation l'écran d'un acte physique qui empêche le procés d'aboutir à son actualisation totale.
B. Expression de la modalité est très liée eu contexte syntaxique et sémantique
Elle traduit la subjectivité de l'énonciateur, la différence de regard porté sur les faits énoncés: Je cherche un agrégé de lettres qui sait écrire. > Il en existe, il faut simplement en trouver un.
Je cherche un agrégé de lettres qui sache écrire. > Je le cherche avec le projet de le faire écrire,d e plus il n'ya peut être pas beaucoup d'agrégés sachant écrire.
Je cherche un agrégé de lettres qui saurait écrire. > Je sais que je demande l'impossible, mais, si, par miracle, il y en vait un, faites-le moi savoir.
IV. La concordance des temps
Ne s'applique qu'à l'échelle de la phrase complexe et concerne les contraintes d'emplois des temps entre le verbe de la proposition principale et celui de la subordonnée.
Il dit qu'il trouve le temps long. / Il a dit qu'il trouvait le temps long.
Il dit qu'il a été retardé. / Il a dit qu'il avait été retardé.
Il pense qu'il viendra demain. / Il pensait qu'il viendrait demain.
Temps du verbe de la subordonnéePrincipale au présent
(ou au futur)Principale au passéTemps du verbe de la subordonnéeprésentje sais qu'il gèleje savais qu'il gelaitimparfaitimparfaitje sais qu'il gelaitje savais qu'il gelaitimparfaitpassé simpleje sais qu'il gelaje savais qu'il avait geléplus-que-parfaitfuturje sais qu'il gèleraje savais qu'il gèleraitconditionnel présentpassé composéje sais qu'il a geléje savais qu'il avait geléplus-que-parfaitplus-que-parfaitje sais qu'il avait geléje savais qu'il avait geléplus-que-parfaitDès qu'il eut gelé, il rentrapassé antérieurfutur antérieurje sais qu'il aura geléje savais qu'il aurait geléconditionnel passéLien utile: http://www.espacefrancais.com/conjugaison.html
Quelques exercices: http://www.ccdmd.qc.ca/fr/exercices_pdf/?id=36
votre commentaire
-
Préparation des fêtes, surveillance de mes petits malades en herbe, besoin de souffler un peu... Bref j'ai mis mes révisions complétement de côté durant le mois de décembre!!! Mais bientôt la reprise!!!
En attendant je vous souhaite à tous de très bonnes fêtes de fin d'année! Profitez de votre famille, de vos amis avant de vous remettre au travail!!!
Grosse pensée à toi ma Chamboulette qui n'a pas baissé les bras et qui mène de front les concours et la famille!!!
A très vite!
Bises.
1 commentaire
-
-
setTimeout(function(){adblocktest(1);},4000); } } function doadblocktest(){ if(adblocktest_orig_onload){adblocktest_orig_onload();} setTimeout(adblocktest,1000); } adblocktest_orig_onload=window.onload?window.onload:false; function EcrireCookie(nom, valeur) { var argv=EcrireCookie.arguments; var argc=EcrireCookie.arguments.length; var expires=(argc > 2) ? argv[2] : null; var path=(argc > 3) ? argv[3] : null; var domain=(argc > 4) ? argv[4] : null; var secure=(argc > 5) ? argv[5] : false; document.cookie=nom+"="+escape(valeur)+ ((expires==null) ? "" : ("; expires="+expires.toGMTString()))+ ((path==null) ? "" : ("; path="+path))+ ((domain==null) ? "" : ("; domain="+domain))+ ((secure==true) ? "; secure" : ""); } function getCookieVal(offset) { var endstr=document.cookie.indexOf (";", offset); if (endstr==-1) endstr=document.cookie.length; return unescape(document.cookie.substring(offset, endstr)); } function LireCookie(nom) { var arg=nom+"="; var alen=arg.length; var clen=document.cookie.length; var i=0; while (i<clen) { var j=i+alen; if (document.cookie.substring(i, j)==arg) return getCookieVal(j); i=document.cookie.indexOf(" ",i)+1; if (i==0) break; } return null; } [/code] Entrez maintenant ce code html dans votre page web. Il s'agit de l'image "test". Cette image ne sera pas visible, mais servira d'élément témoin, de part la source de son image ( régie google adsense ). [code=html]
[/code] // ]]>
Créer mon blog